LTspiceでディジタル・フィルタを確認する

■問題
使用するコマンド ― .AC

小川　敦　Atsushi Ogawa

　図1は，移動平均フィルタと呼ばれるディジタル・フィルタのブロック図です．4つの遅延回路は，入力信号をサンプリング周期Tだけ遅延させ，4つの遅延した(過去の)信号の値を出力します．遅延回路の右側にある平均回路は，入力信号と4つの遅延信号を加算し，5分の1にした値を出力します．
　この移動平均フィルタは，ローパス・フィルタと特定の周波数の信号を減衰させるノッチ・フィルタとして動作します．サンプリング周波数をf_S=1/Tとしたとき，ノッチ周波数(f_n)の式として正しいのは(a)～(d)のどれでしょうか．

図1　移動平均フィルタのブロック図
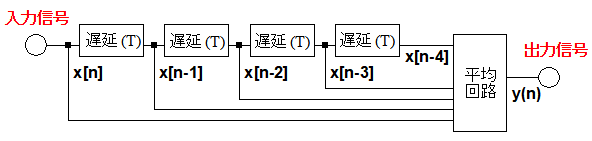
x[n]，y[n]は時間nのときのデータで，x[n-1]はnよりも1サンプリング周期前（過去）の信号を表している．

(a) f_n=fs/4　(b) f_n=fs/5　(c) f_n=fs/6　(d) f_n=fs/7

■ヒント

　正弦波信号の1周期分の平均値を計算すると，その結果は0になります．図1の回路ではどのように平均値を計算しているかを考えれば，答えは簡単に分かります．

■解答

(b) f_n=fs/5

　図1の平均回路では，入力信号と4つの遅延信号を加算し，5分の1にした値を計算しています．遅延回路1つの遅延時間はTなので，5Tの期間の信号の平均値を計算していることになります．
　もし，1周期が5Tの正弦波信号が入力されると，その平均値は0になり，出力されないことになります．周期が5Tの信号の周波数は「f_n=1/(5T)=fs/5」となり，これがノッチ・周波数になります．

■解説

●アナログ信号とディジタル信号
　アナログ信号は，図2(a)のような時間的に連続したものです．また，ディジタル信号は，図2(b)のようなサンプリング周期(T)ごとにとびとびになっています．サンプリング周期の逆数がサンプリング周波数f_Sです．サンプリング周波数は，入力信号周波数の2倍よりも大きくする必要があります．また，ディジタル信号は縦軸の値も連続ではなく，分解能に応じたとびとびの値となります．ここでは，分解能は十分高いものとして扱います．

図2　アナログ信号とディジタル信号の違い
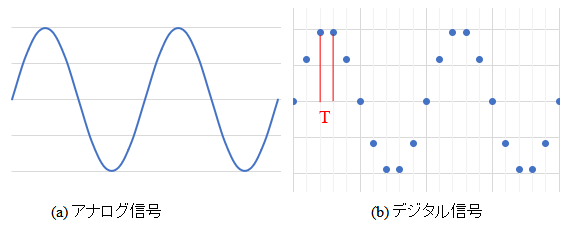
ディジタル信号はサンプリング周期(T)ごとにとびとびになっている.

●移動平均フィルタのローパス特性
　アナログ・フィルタは，抵抗やコンデンサで構成します．ディジタル・フィルタは，遅延回路と演算回路で構成します．遅延回路を使用することで，数サンプル前のデータと現在のデータの演算を行うことができます．
　ディジタル・フィルタの中で，もっともシンプルなものが，移動平均フィルタです．図3は，Excelで作成した，移動平均フィルタの効果を確認するためのグラフです．分かりやすくするために，データ間を線で接続しています．
　青色のデータは，必要とする信号に，それよりも高い周波数のノイズが混入した入力信号です．オレンジ色のデータはそれぞれ，x[n]，x[n-1]，x[n-2]，x[n-3]，x[n-4]の5点のデータの平均を計算したものです．遅延素子を4つ使用した，図1の移動平均フィルタの出力に相当するものになります．5点のデータの平均値をとることで，ノイズ成分が減少していることが分かります．図3から分かるように，移動平均フィルタは高い周波数成分を減衰させる，ローパス・フィルタとして動作します．

図3　移動平均フィルタの効果を確認するためのグラフ
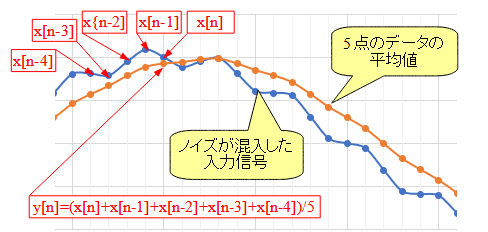
5点のデータの平均値をとることで，ノイズが減少していることが分かる.

●移動平均フィルタのノッチ特性
　移動平均フィルタは，ローパス・フィルタとして動作すると共に，ノッチ・フィルタとしても動作します．図4は，移動平均フィルタがノッチ・フィルタとしても動作することを確認するためのグラフです．青色の入力信号の周波数(f)はf=1/(5T)となっています．オレンジ色が，遅延回路を4つ使用した図1の移動平均フィルタの出力に相当するものです．x[n]，x[n-1]，x[n-2]，x[n-3]，x[n-4]の5点のデータの平均を計算したものになっています．

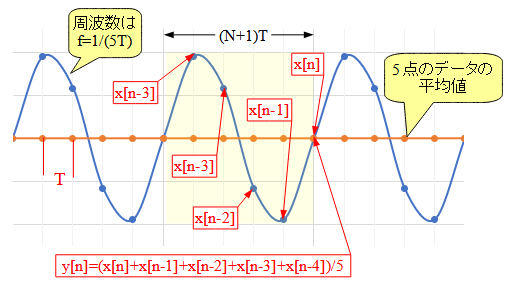
図4　移動平均フィルタがノッチ・フィルタとなることを確認するためのグラフ
5点のデータの平均値は0になる．

　図4を見ると分かるように，入力信号の1周期（黄色ハッチング部分）が5Tなので，その1周期の中のデータの平均値は0になります．つまり，図1の移動平均フィルタでは，周波数1/(5T)の信号は出力に現れず，ノッチ周波数(f_n)は1/(5T)になります．サンプリング周波数をf_Sとし，移動平均フィルタに使用する遅延回路の段数をNとすると，ノッチ周波数(f_n)は式1で表されます．

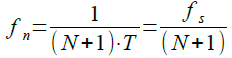・・・・・・・・・・・・・・・・・・・・・・・・・・・(1)

●LTspiceで移動平均フィルタを確認する
　図5は，図1の移動平均フィルタの周波数特性をLTspiceでシミュレーションするための回路です．X1～X4は遅延回路です．fsという変数の値を250としていますが，これはサンプリング周波数に相当するものです．そして，fsの逆数をTという変数に代入し，遅延時間を設定しています．

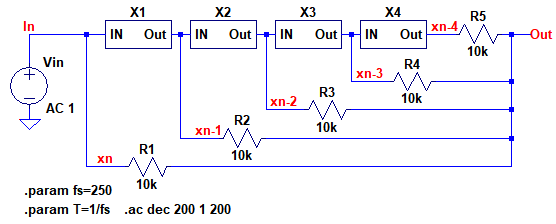
図5　移動平均フィルタの周波数特性をLTspiceでシミュレーションするための回路
X1～X4は遅延回路で，R1～R5により平均値を出力する．

　遅延回路（X1～X4）の中は図6のようにB電源(bitrary Behavioral Voltage )を使用した回路になっています．V=Delay(V(IN)，T)とすることで，IN端子の電圧を，Tという変数で指定した時間だけ遅延させ，Out端子に出力します．
　ここで，IN端子の[Port Type]はInputとし，Out端子の[Port Type]はOutputとしてあります．LTspiceで，階層設計用のシンボルを作るときは，使用する回路図を名前を付けて保存し，上部のメニューから[Hirearchy][Open this Sheet's Symbol]を選択します．すると，自動的にシンボルを作るか聞かれるので，OKボタンを押すと，回路図と同じ名前のシンボルが作成されます．図5では，このようにして作成したシンボルを使用しています．

図6　B電源を使用した遅延回路
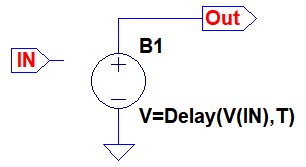
遅延時間はTという変数で指定する．

　図5のR1～R5でそれぞれの信号を加算し，1/5とすることでOut端子には平均値が出力されます．図7は，R1～R5により平均値が出力されることを説明するための回路図です．

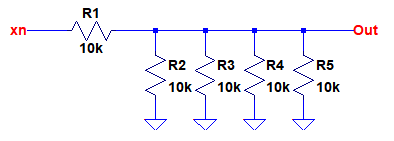
図7　R1～R5により平均値が出力されることを説明するための回路
V(xn)はR1と「R2～R5の並列抵抗」で分圧される．

　図5において，V(xn)のみ信号があり，それ以外のV(xn-1)～V(xn-4)が0Vだったとすると，図7の回路と等価になります．図7において，V(xn)はR1と「R2～R5の並列抵抗」で分圧されます．そのため，R1～R5の抵抗値をRとすると，V(Out)は式2のようになります．

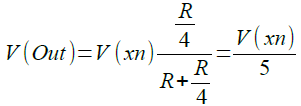・・・・・・・・・・・・・・・・・・・・・・(2)

　V(xn-1)等でも同様な式となり，それぞれの信号を重ね合わせると，V(Out)は式3で表されます．

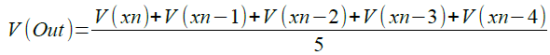・・・・・(3)

　式3のように，Out端子には5つの信号の平均値が出力されることになります．

●移動平均フィルタの周波数特性をLTspiceで確認する
　図8は，図5の移動平均フィルタの周波数特性のシミュレーション結果です．

図8　移動平均フィルタの周波数特性のシミュレーション結果
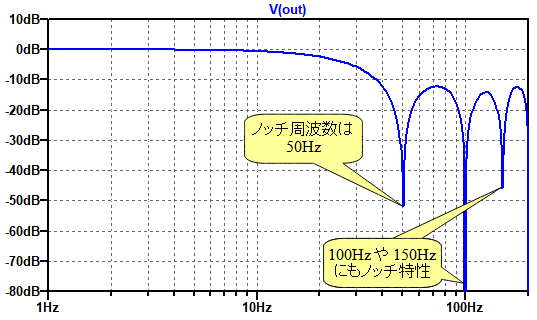
サンプリング周波数(f_S)を250Hzとしたため，ノッチ周波数は50Hzとなっている．

　サンプリング周波数(f_S)を250Hzとしたため，移動平均フィルタのノッチ周波数は式4のように50Hzとなります．シミュレーションでもノッチ周波数は50Hzとなっています．

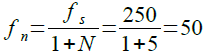・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　なお，ノッチ特性は，50Hzだけでなく，その倍数である100Hzや150Hzでも見られます．家庭用電源から発生するハム・ノイズのようなものは，ひずんで高調波成分が含まれていることがあります．また，図8のような特性は，高調波成分を含んだノイズに対しても有効です．
　以上，移動平均フィルタについて解説しました．アナログ・フィルタは，アナログ回路を組み合わせることで，さまざまな特性のフィルタが作れます．同様に，ディジタル・フィルタも遅延回路や演算回路を組み合わせることで，さまざまな特性のフィルタを作ることができます．